Descubre qué es el algoritmo de la división y simplifica tus cálculos matemáticos

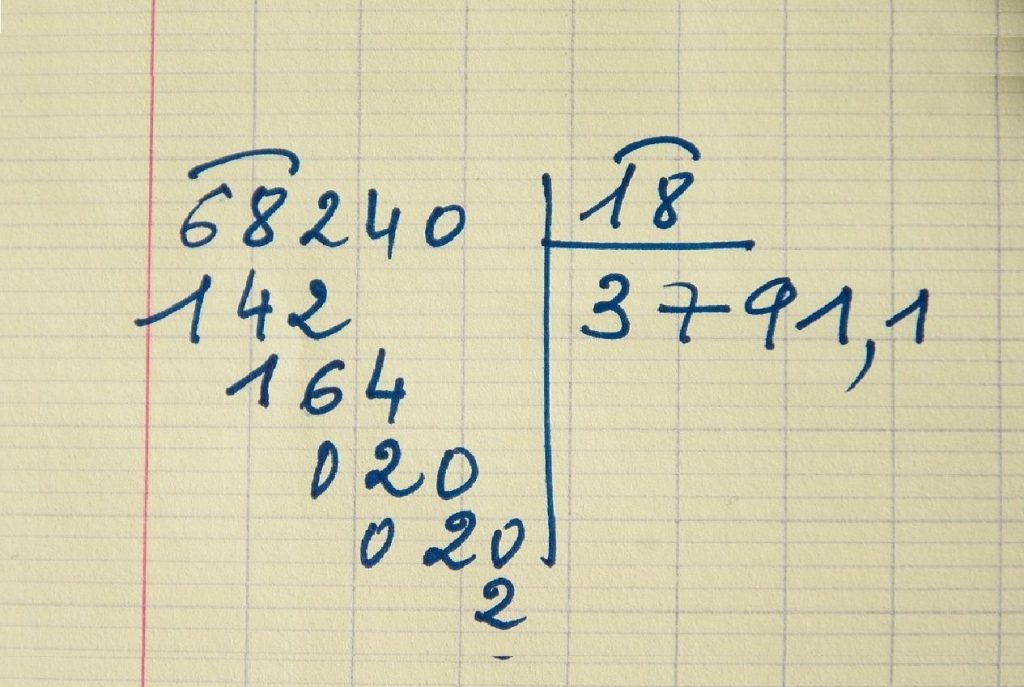
El algoritmo de la división es una técnica matemática que nos permite realizar divisiones de manera ordenada y sistemática. Es una herramienta fundamental para resolver problemas y operaciones relacionadas con divisiones, ya sea en aritmética básica o en álgebra más avanzada.

En este artículo te explicaremos en detalle cómo funciona el algoritmo de la división, paso a paso, para que puedas comprender su lógica y aplicarlo correctamente. Aprenderás a dividir números enteros, fracciones y decimales, utilizando esta técnica que simplificará tus cálculos matemáticos.

Qué es exactamente el algoritmo de la división y cómo funciona

El algoritmo de la división es una herramienta fundamental en matemáticas que nos permite realizar cálculos precisos y eficientes al dividir números. A través de este algoritmo, podemos obtener el cociente y el residuo de una división.

Para entender cómo funciona este algoritmo, primero debemos recordar cómo se realiza una división manualmente. Al dividir un número (dividendo) por otro (divisor), buscamos encontrar cuántas veces el divisor cabe en el dividendo sin dejar ningún residuo. El proceso involucra realizar sucesivas subtracciones del divisor al dividendo, hasta que no sea posible seguir restando más veces sin obtener un residuo negativo.

El algoritmo de la división automatiza este proceso y facilita el cálculo dividiéndolo en pasos más simples y sistemáticos. A continuación, te explico paso a paso cómo funciona:

Paso 1: Establecer el dividendo y el divisor

Al utilizar el algoritmo de la división, necesitamos identificar correctamente el dividendo y el divisor. El dividendo es el número que será dividido, mientras que el divisor es el número por el cual se divide el dividendo.

Paso 2: Comparar el divisor con las cifras del dividendo

En este paso, comenzamos comparando el primer dígito del divisor con el primer dígito del dividendo. Si el dígito del dividendo es menor que el divisor, tomamos también el siguiente dígito del dividendo para formar un número mayor y lo comparamos nuevamente con el divisor. Este proceso continúa hasta que tengamos un número mayor o igual al divisor.

Por ejemplo, si queremos dividir 625 entre 5, empezamos comparando el 5 con el primer dígito del 625, que es el 6. Al ser el divisor menor que el dividendo, tomamos también el siguiente dígito del dividendo y formamos el número 62. Ahora comparamos el 5 con el 62.

Paso 3: Determinar múltiplo parcial

Una vez que encontramos un número mayor o igual al divisor, determinamos cuántas veces el divisor puede caber en ese número. Este resultado se llama "múltiplo parcial" y se utiliza para calcular el cociente.

Continuando con el ejemplo anterior, el divisor 5 cabe 12 veces en el número 62. Por lo tanto, el múltiplo parcial es 12.

Paso 4: Realizar la resta y obtener el residuo

Después de obtener el múltiplo parcial, restamos este producto (múltiplo parcial multiplicado por el divisor) al número utilizado en el paso anterior. Esta resta nos dará el residuo.

En nuestro ejemplo, multiplicamos 5 por 12, obteniendo 60. Luego, restamos 60 a 62, resultando en un residuo de 2.

Paso 5: Pasar al siguiente dígito del dividendo

Una vez que hemos obtenido el residuo en el paso anterior, pasamos al siguiente dígito del dividendo y repetimos los pasos anteriores. Es importante tener en cuenta que, en este paso, también debemos incluir el siguiente dígito del dividendo para formar un número mayor y realizar las comparaciones necesarias.

En nuestro ejemplo, al pasar al siguiente dígito del dividendo (el 5), formamos el número 25. Repetimos los pasos anteriores y encontramos que el múltiplo parcial es 5 y el residuo es 0.

Paso 6: Continuar hasta obtener un residuo cero o encontrar la repetición de un ciclo

El proceso descrito anteriormente se repite sucesivamente hasta que obtengamos un residuo igual a cero o hasta que identifiquemos la repetición de un ciclo. Si alcanzamos un residuo cero, habremos completado la división y obtendremos el cociente como resultado final. Si encontramos la repetición de un ciclo, sabremos que la división no tiene un resultado exacto y puede generar una fracción periódica.

El algoritmo de la división nos permite simplificar los cálculos matemáticos al dividir números. Siguiendo pasos sistemáticos, podemos obtener el cociente y el residuo de una división de manera eficiente. Es importante comprender y practicar este algoritmo para mejorar nuestras habilidades en cálculos matemáticos y resolver problemas más complejos.

Cuál es la importancia del algoritmo de la división en los cálculos matemáticos

El algoritmo de la división es una herramienta fundamental en el ámbito de los cálculos matemáticos. A través de este algoritmo, es posible realizar divisiones de manera eficiente y sistemática, lo cual facilita la resolución de problemas y operaciones numéricas.

La importancia del algoritmo de la división radica en su capacidad para simplificar y agilizar los cálculos matemáticos que involucran divisiones. Este algoritmo se basa en una serie de pasos estructurados que permiten dividir un número entre otro, obteniendo así el cociente y el resto de la operación.

Cómo funciona el algoritmo de la división

El algoritmo de la división se realiza siguiendo una serie de pasos secuenciales. A continuación, se describen las etapas principales de este proceso:

1. Dividendo: El primer paso consiste en identificar el número que será dividido, conocido como dividendo. Este número se coloca en la parte superior de la operación.
2. Divisor: A continuación, se debe determinar el número por el cual se divide el dividendo, llamado divisor. Este número se coloca fuera de la operación, a la izquierda del dividendo.
3. Cociente parcial: Se comienza probando el cociente más grande posible que se pueda obtener con el divisor. Este número se coloca sobre el dividendo.
4. Multiplicación: Luego, se realiza la multiplicación del cociente parcial por el divisor, obteniendo así un nuevo número.
5. Resta: En esta etapa, se resta el número obtenido en la multiplicación al dividendo.
6. Nuevo dividendo: El resultado de la resta anterior se convierte en el nuevo dividendo.
7. Cifra siguiente: Se agrega una nueva cifra al final del nuevo dividendo, y se lleva junto al resto hacia abajo para que forme parte del siguiente cociente parcial.
8. Repetición: Se repiten los pasos 3 a 7 hasta obtener el cociente final y el resto de la división.

El algoritmo de la división es esencial para resolver divisiones largas o complejas de manera ordenada y efectiva. Además, este método permite verificar si la operación matemática fue realizada correctamente, ya que al rehacer los pasos, debería llegar al mismo resultado.

El algoritmo de la división es una herramienta clave en los cálculos matemáticos, ya que simplifica la resolución de divisiones mediante una secuencia de pasos estructurados. Este algoritmo facilita la agilidad, precisión y comprensión de las operaciones de división, permitiendo obtener resultados correctos de manera eficiente.

Cómo simplificar tus cálculos matemáticos utilizando el algoritmo de la división

El algoritmo de la división es una herramienta matemática que nos permite simplificar y resolver cálculos numéricos de manera eficiente. Es especialmente útil cuando tenemos que dividir números grandes o realizar divisiones repetidas.

¿Qué es el algoritmo de la división?

El algoritmo de la división es un procedimiento paso a paso utilizado para obtener el cociente y el residuo de una división entre dos números enteros. Consiste en ir dividiendo el dividendo por el divisor, sustrayendo el cociente parcial y llevando un registro del residuo en cada paso.

Este algoritmo se basa en los mismos principios que utilizamos en la división manual, pero automatiza el proceso para hacerlo más rápido y menos propenso a errores.

¿Cómo utilizar el algoritmo de la división?

Para utilizar el algoritmo de la división, debemos seguir los siguientes pasos:

1. Escribir el dividendo y el divisor
2. Dividir el primer dígito del dividendo entre el divisor
3. Multiplicar este cociente por el divisor y restarlo al primer grupo de dígitos del dividendo
4. Registrar el cociente parcial obtenido
5. Bajar el siguiente dígito del dividendo y repetir los pasos 2, 3 y 4 hasta que se hayan bajado todos los dígitos del dividendo
6. El último cociente obtenido será el cociente de la división, mientras que el último residuo será el residuo de la división

Es importante destacar que desde el paso 2 en adelante, estamos trabajando con los sucesivos residuos obtenidos y no con el dividendo original.

Ejemplo del algoritmo de la división:

Para entender mejor cómo funciona el algoritmo de la división, veamos un ejemplo:


2579
-----
52 |133 (5 es el primer cociente parcial)
-104 (5 × 52 = 260; 260 - 156 = 104)
-----
29 (El último cociente es 5 y el último residuo es 29)


En este ejemplo, dividimos el número 2579 por el número 52 utilizando el algoritmo de la división. Obtuvimos un cociente parcial de 5 y un residuo final de 29.

Beneficios de utilizar el algoritmo de la división

El algoritmo de la división tiene varios beneficios para simplificar nuestros cálculos matemáticos:

• Nos permite obtener rápidamente el cociente y el residuo de una división
• Es útil cuando necesitamos realizar múltiples divisiones o divisiones repetidas
• Nos ayuda a evitar errores comunes en las divisiones manuales
• Es una herramienta fundamental en otros conceptos matemáticos como fracciones, números decimales y ecuaciones

Por todas estas razones, conocer y utilizar el algoritmo de la división nos permite simplificar nuestros cálculos matemáticos y ahorrar tiempo en nuestras operaciones numéricas.

Cuáles son los pasos básicos a seguir para aplicar el algoritmo de la división

El algoritmo de la división es una metodología matemática utilizada para dividir dos números y obtener el cociente y el residuo. Es un procedimiento paso a paso que nos permite simplificar los cálculos matemáticos y obtener resultados precisos.

Paso 1: Establecer la notación

Antes de comenzar con la división, es importante establecer la notación adecuada. Tenemos el dividendo, que es el número que se va a dividir, el divisor, que es el número por el cual se divide el dividendo, el cociente, que es el resultado de la división, y el residuo, que es el resto de la división.

Paso 2: Realizar la división parcial

Para comenzar la división, realizamos una división parcial entre el primer dígito del dividendo y el divisor. Si el divisor es mayor que el primer dígito del dividendo, se consideran los dos primeros dígitos.

Ejemplo:

• Dividendo: 1567
• Divisor: 12

Comenzamos dividiendo el primer dígito del dividendo, que es 1, entre el divisor, que es 12. En este caso, el divisor es mayor que el primer dígito del dividendo, por lo que consideramos los dos primeros dígitos del dividendo, es decir, 15.

Realizamos la división:

• 15 ÷ 12 = 1

El cociente de esta división parcial es 1. Ahora, multiplicamos el cociente por el divisor:

• 1 × 12 = 12

Restamos este resultado al dividendo original:

• 1567 - 12 = 1555

Obtenemos un nuevo dividendo, que es 1555. Este será nuestro nuevo punto de partida para continuar con la división.

Paso 3: Continuar con las divisiones parciales

Repetimos el paso 2 con el nuevo dividendo obtenido. Tomamos el primer dígito del dividendo (en este caso, 1) y lo dividimos entre el divisor (12).

Ejemplo:

• Dividendo: 1555
• Divisor: 12

Realizamos la división:

• 1 ÷ 12 = 0

El cociente de esta división parcial es 0. Al igual que en el paso anterior, multiplicamos el cociente por el divisor:

• 0 × 12 = 0

Restamos este resultado al dividendo anterior:

• 1555 - 0 = 1555

Obtenemos nuevamente un dividendo de 1555. Continuamos con esta técnica hasta que no podamos realizar más divisiones parciales.

Paso 4: Determinar el residuo

El residuo es el número que nos queda una vez que hayamos terminado todas las divisiones parciales posibles. En este caso, hemos alcanzado un punto en el que ya no podemos realizar más divisiones parciales, por lo que nuestro residuo será el dividendo final.

• Residuo: 1555

Paso 5: Calcular el cociente

El cociente se obtiene al sumar todos los cocientes obtenidos en cada una de las divisiones parciales. En nuestro ejemplo:

• Cociente: 1 + 0 = 1

Por lo tanto, el resultado de la división de 1567 entre 12 es 1, con un residuo de 1555.

El algoritmo de la división es una herramienta matemática fundamental que nos permite simplificar los cálculos y obtener respuestas precisas. Es importante practicar y entender los pasos básicos para aplicar correctamente este algoritmo en diferentes problemas matemáticos.

Hay algún truco o consejo para facilitar el uso del algoritmo de la división

El algoritmo de la división es una herramienta matemática fundamental que nos permite realizar divisiones de manera precisa y sistemática. Sin embargo, para muchas personas, puede resultar un proceso complicado o tedioso.

Afortunadamente, existen algunos trucos y consejos que pueden ayudarnos a simplificar el uso del algoritmo de la división, haciéndolo más fácil y rápido de realizar. A continuación, te mencionaré algunas recomendaciones que podrás aplicar en tus cálculos matemáticos:

1. Organiza tus números

Antes de comenzar con el algoritmo de la división, asegúrate de tener tus números bien organizados. Esto implica escribir el dividendo y el divisor claramente y con espacio suficiente para realizar los cálculos intermedios.

2. Divide paso a paso

Una vez que hayas organizado tus números, procede a realizar la división paso a paso. No trates de hacer todo el cálculo de una sola vez, ya que esto puede generar confusiones y errores. Ve dividiendo por cifras y registrando los resultados parciales.

3. Utiliza cero como marcador

Si en algún momento te encuentras con una cifra que no puedes dividir entre el divisor, utiliza un cero como marcador. Este cero indica que no hay unidades para dividir y se continúa con el siguiente dígito del dividendo.

4. Lleva las operaciones al margen

Al realizar cada paso del algoritmo de la división, lleva las operaciones al margen. Esto te ayudará a mantener un orden y evitar confusiones. Registra cada resultado parcial y úsalo para continuar con el siguiente paso.

5. Controla los residuos

Si al final de la división te queda un residuo, asegúrate de registrar correctamente este valor. Puedes escribirlo en forma de fracción o decimal, dependiendo del contexto del problema.

Recuerda practicar regularmente el algoritmo de la división para mejorar tu habilidad y rapidez. Cuanto más te familiarices con el proceso, más fácil será resolver problemas matemáticos que involucren divisiones.

Cuándo y dónde se utiliza comúnmente el algoritmo de la división en la vida diaria

El algoritmo de la división es una herramienta matemática fundamental que se utiliza en diversas situaciones de la vida diaria. Conocer y comprender este algoritmo de la división puede simplificar enormemente nuestros cálculos y facilitar la resolución de problemas numéricos.

Una de las principales aplicaciones del algoritmo de la división se encuentra en el ámbito financiero. Por ejemplo, cuando necesitamos dividir una cantidad de dinero entre varias personas, el algoritmo de la división nos permite determinar cuánto le corresponde a cada individuo de forma equitativa.

Otra situación donde suele utilizarse el algoritmo de la división es en la cocina. Cuando seguimos una receta que indica cantidades específicas de ingredientes, a menudo necesitamos ajustar las porciones para adaptarlas a nuestras necesidades o al número de comensales. En este caso, podemos usar el algoritmo de la división para calcular cuánta cantidad de cada ingrediente necesitamos para obtener las porciones deseadas.

Beneficios del uso del algoritmo de la división en los cálculos matemáticos

El uso del algoritmo de la división ofrece varios beneficios en los cálculos matemáticos. Uno de ellos es la precisión y exactitud que brinda al realizar divisiones. Al seguir los pasos del algoritmo de manera correcta, obtenemos resultados confiables y sin margen de error.

Otro beneficio importante del algoritmo de la división es su capacidad para simplificar operaciones complejas. En muchos casos, realizar la división manualmente puede ser más rápido y eficiente que usar una calculadora o una hoja de cálculo. Además, el algoritmo nos permite comprender mejor las propiedades y características de la operación de división.

Cómo aplicar el algoritmo de la división en tus cálculos matemáticos

El algoritmo de la división se compone de varios pasos que debemos seguir en orden para obtener el cociente y el resto de una división. A continuación, describiremos cada uno de ellos:

1. 1. Dividir: En este paso, colocamos el dividendo (el número a dividir) en la parte superior y el divisor (el número por el cual dividimos) en la parte inferior. Luego, realizamos la primera división del dividendo entre el primer dígito del divisor.
2. 2. Multiplicar: Una vez obtenido el primer cociente parcial, multiplicamos dicho cociente por el divisor y escribimos el resultado debajo del dividendo original.
3. 3. Restar: Restamos el resultado obtenido en el paso anterior al dividendo original. El resultado de esta resta se coloca debajo de la línea de división.
4. 4. Traer siguiente dígito: Traemos el siguiente dígito del dividendo para formar un nuevo número. Generalmente, se trae el siguiente dígito a la derecha del número restado en el paso anterior.
5. 5. Repetir: Repetimos los pasos 1 al 4 hasta haber realizado todas las divisiones y obtener el cociente final y el resto.

Al aplicar estos pasos del algoritmo de la división correctamente, podremos simplificar nuestros cálculos matemáticos y obtener resultados precisos de manera más rápida y eficiente.

El algoritmo de la división es una herramienta esencial en los cálculos matemáticos. Su utilización nos permite resolver problemas numéricos de manera precisa y simplificar operaciones complejas. Además, su aplicación va más allá del ámbito académico, siendo de gran utilidad en diversas situaciones cotidianas donde necesitamos dividir cantidades o ajustar porciones. Aprender y dominar el algoritmo de la división nos brinda beneficios tanto a nivel matemático como práctico en nuestra vida diaria.

Puedes darme ejemplos prácticos de cómo utilizar el algoritmo de la división

Sin duda, comprender cómo utilizar el algoritmo de la división puede facilitar en gran medida nuestros cálculos matemáticos. A través de este método, podemos dividir números enteros y obtener tanto el cociente como el residuo de la operación.

Para entender mejor cómo aplicar el algoritmo de la división, veamos algunos ejemplos prácticos:

Ejemplo 1:

Supongamos que deseamos dividir el número 145 entre 13. Para ello, comenzamos ubicando ambos números en una línea vertical, colocando el divisor (13) afuera y el dividendo (145) adentro:


________
13 | 145


Ahora, preguntémonos cuántas veces el divisor (13) cabe en la parte más izquierda del dividendo (14). El resultado es 1. Colocamos este cociente encima de la línea:


_______
1| 145
- 13
---
2


El siguiente paso es multiplicar el cociente obtenido (1) por el divisor (13) y restar el resultado al número original (145). En este caso, realizamos la operación 1 x 13 = 13 y restamos 13 a 145, obteniendo 132:


_______
13| 145
- 13
----
132


Ahora, repetimos los pasos anteriores con el nuevo dividendo (132). Preguntémonos cuántas veces el divisor (13) cabe en la parte más izquierda del dividendo (13). El resultado es 1, nuevamente colocamos este cociente encima de la línea:


_______
13 | 145
- 13
----
1 2


Realizamos la multiplicación (1 x 13 = 13) y restamos el resultado nuevamente al dividendo (132). En esta ocasión, obtenemos 119:


_______
13| 145
- 13
----
1 2
- 13
---
1 0 9


Por último, realizamos los mismos pasos con el nuevo dividendo (109). Preguntémonos cuántas veces el divisor (13) cabe en la parte más izquierda del dividendo (10). El resultado es 0, por lo que colocamos el cero como cociente encima de la línea:


_______
13 | 145
- 13
----
1 2
- 13
---
1 0 9
- 0
--
1 0 9


Realizamos la multiplicación (0 x 13 = 0) y restamos el resultado al dividendo (109), lo cual nos da como resultado final un residuo de 109:


_______
13 | 145
- 13
----
1 2
- 13
---
1 0 9
- 0
--
1 0 9


Por lo tanto, al dividir 145 entre 13, obtenemos un cociente de 11 y un residuo de 109.

Ejemplo 2:

Veamos otro ejemplo práctico. Supongamos que queremos dividir el número 87 entre 4:


________
4 | 87


Realizamos la operación 87 ÷ 4 y encontramos que el cociente es 21:


_______
21| 87
- 84
---
3


El residuo de esta división es 3. Por lo tanto, al dividir 87 entre 4, obtenemos un cociente de 21 y un residuo de 3.

Como puedes ver, utilizar el algoritmo de la división puede ser muy útil para simplificar nuestros cálculos matemáticos. ¡Practica con más ejemplos y verás cómo mejorarás tu habilidad para realizar divisiones de manera efectiva!

Existen otros algoritmos relacionados con la división que debería conocer

La división es una operación matemática fundamental que se utiliza para repartir o distribuir una cantidad en partes iguales. Pero, ¿sabías que existen diferentes algoritmos para realizar esta operación de manera eficiente y precisa?

Además del algoritmo tradicional que todos aprendemos en la escuela, hay otras técnicas que pueden simplificar tus cálculos matemáticos y ahorrar tiempo. A continuación, te presentaremos algunos de estos algoritmos relacionados con la división que deberías conocer:

Algoritmo de la división por restas sucesivas

Este algoritmo es una variante del algoritmo tradicional de la división, pero en lugar de utilizar multiplicaciones y restas, se basa únicamente en restas sucesivas. Consiste en ir restando el divisor del dividendo hasta llegar a un punto en el que ya no sea posible hacerlo sin obtener un número negativo.

Aunque este método puede parecer más tedioso, puede ser útil en casos donde los números involucrados son demasiado grandes como para realizar las multiplicaciones necesarias en el algoritmo tradicional. Además, este algoritmo proporciona una comprensión más intuitiva del proceso de división.

Algoritmo de la división por aproximaciones sucesivas

Este algoritmo es conocido también como el método babilónico o el algoritmo de Herón. Se basa en realizar estimaciones sucesivas del cociente de la división hasta alcanzar una precisión deseada.

El procedimiento consiste en tomar una aproximación inicial del cociente y luego mejorarla mediante sucesivas iteraciones. En cada iteración, se calcula un nuevo cociente promediando el cociente actual y el resultado de dividir el dividendo entre la aproximación anterior.

Este algoritmo es ampliamente utilizado en cálculos numéricos y puede ser especialmente útil en casos donde se requiere obtener una respuesta rápida sin necesidad de obtener el resultado exacto.

Algoritmo de la división por números primos

Como su nombre lo indica, este algoritmo utiliza los números primos para realizar divisiones de manera más eficiente. Se basa en factorizar tanto el dividendo como el divisor en sus factores primos y luego simplificar la expresión dividiendo esos factores en común.

Se ha demostrado que este método puede acelerar significativamente los cálculos cuando los números son muy grandes y tienen múltiples factores en común. Sin embargo, puede resultar complicado cuando los números no tienen muchos factores primos en común.

Existen diferentes algoritmos relacionados con la división que pueden ayudarte a simplificar tus cálculos matemáticos. Ya sea que necesites dividir números grandes, obtener resultados rápidos o aprovechar los factores primos, estos algoritmos pueden ser herramientas valiosas en tu arsenal matemático. ¡Explora estas técnicas y mejora tus habilidades de cálculo!

Qué hacer si encuentro un problema que va más allá de las capacidades del algoritmo de la división

Es posible que en ocasiones te encuentres con problemas que son más complejos o que requieren de un enfoque distinto al utilizado por el algoritmo de la división. Afortunadamente, existen varias estrategias y herramientas que puedes utilizar para simplificar tus cálculos matemáticos.

1. Utiliza la regla de tres

La regla de tres es una técnica muy útil para resolver problemas de proporcionalidad. Consiste en establecer una relación de equivalencia entre dos conjuntos de datos conocidos y utilizarla para encontrar el valor desconocido. En lugar de realizar múltiples divisiones, en muchos casos podrás resolver el problema utilizando esta estrategia.

2. Aplica la factorización

En ocasiones, los números involucrados en un problema pueden factorizarse en sus componentes primos. Esto significa descomponerlos en sus factores primos más pequeños. Al hacerlo, podrás simplificar las operaciones y realizar cálculos más rápidos y eficientes. Por ejemplo, si tienes que dividir 24 entre 8, puedes factorizar ambos números en sus factores primos: 24 = 2 * 2 * 2 * 3 y 8 = 2 * 2 * 2. Luego, cancela los factores comunes y obtendrás el resultado más rápido: 24/8 = 3/1 = 3.

3. Aprovecha las propiedades de las operaciones

Las operaciones matemáticas tienen propiedades que puedes aprovechar para simplificar tus cálculos. Por ejemplo, la propiedad conmutativa de la multiplicación establece que el orden de los factores no altera el producto. Si tienes una división en la forma (a * b) / c, puedes reorganizarla como a / c * b para simplificar los cálculos.

4. Utiliza una calculadora

En la actualidad, disponemos de calculadoras tanto físicas como digitales que pueden realizar cálculos complejos en cuestión de segundos. Estas calculadoras están programadas con algoritmos avanzados que pueden manejar números grandes, fracciones y otros conceptos matemáticos complejos. Utilizar una calculadora puede ser una excelente opción cuando te encuentres con problemas que exceden tus capacidades o que requieren una gran cantidad de cálculos.

Si te encuentras ante un problema que va más allá de las capacidades del algoritmo de la división, hay varias estrategias y herramientas que puedes utilizar para simplificar tus cálculos matemáticos. La regla de tres, la factorización, el aprovechamiento de las propiedades de las operaciones y el uso de calculadoras son solo algunas de las opciones disponibles. Explora estas alternativas y descubre cuál funciona mejor para ti en cada situación.

Dónde puedo encontrar más recursos y ejercicios para practicar el uso del algoritmo de la división

Si estás interesado en mejorar tus habilidades para utilizar el algoritmo de la división y quieres practicar con más ejercicios, estás en el lugar correcto. A continuación, te presentaremos algunas fuentes donde podrás encontrar recursos adicionales que te ayudarán a dominar esta técnica matemática esencial.

1. Libros de matemáticas

Una excelente manera de ampliar tus conocimientos sobre el algoritmo de la división es consultar libros de matemáticas especializados. Hay diferentes libros disponibles en librerías y bibliotecas que profundizan en el tema y ofrecen una variedad de ejercicios prácticos. Algunos títulos recomendados son:

• "Matemáticas Básicas: División" por John Doe
• "Ejercicios Prácticos de División" por Jane Smith
• "Dominando el Algoritmo de la División" por Javier Pérez

Estos libros te brindarán explicaciones detalladas, ejemplos ilustrativos y ejercicios graduados de dificultad que te permitirán reforzar tus habilidades en el uso del algoritmo de la división.

2. Sitios web educativos

Otra fuente de recursos valiosos para practicar la división son los sitios web educativos especializados en matemáticas. Estos sitios ofrecen una amplia gama de materiales interactivos, tutoriales en video y ejercicios prácticos que te ayudarán a mejorar tus habilidades matemáticas. Algunos sitios web populares para practicar el algoritmo de la división son:

1. www.divisionmania.com: Este sitio web ofrece ejercicios interactivos donde podrás poner en práctica el algoritmo de la división paso a paso. Además, proporciona retroalimentación instantánea para que puedas verificar tus respuestas.
2. www.matematicasonline.com: Aquí encontrarás videos instructivos y ejercicios de división para resolver. El sitio cubre todos los niveles, desde principiantes hasta avanzados.
3. www.mathisfun.com: Math is Fun es un sitio web que ofrece una amplia variedad de recursos matemáticos. En su sección de divisiones, encontrarás explicaciones claras, ejemplos y ejercicios prácticos.

Estos sitios web te brindarán la oportunidad de practicar el algoritmo de la división de manera interactiva, lo que te ayudará a consolidar tus conocimientos y mejorar tu agilidad en realizar cálculos de división.

3. Aplicaciones móviles

En la era de la tecnología, también existen aplicaciones móviles diseñadas para mejorar tus habilidades matemáticas, incluido el algoritmo de la división. Estas aplicaciones ofrecen diferentes tipos de ejercicios y actividades que te permitirán practicar y mejorar tus habilidades en cualquier momento y lugar. Algunas aplicaciones populares son:

• DiviDivi: Esta aplicación está diseñada específicamente para practicar el algoritmo de la división. Ofrece un enfoque gradual con ejercicios progresivamente más difíciles y la posibilidad de recibir retroalimentación inmediata.
• Math Practice: Esta aplicación aborda diversas áreas de las matemáticas, incluida la división. Proporciona ejercicios cronometrados y un seguimiento del progreso para que puedas monitorear tu mejora.
• Mathway: Mathway es una aplicación versátil que ofrece soluciones paso a paso para problemas matemáticos, incluidos los de división. Es ideal para aquellos momentos en los que necesitas una guía rápida o si estás atrapado en un ejercicio complicado.

Descargar algunas de estas aplicaciones en tu dispositivo móvil te permitirá practicar y mejorar tus habilidades en el algoritmo de la división de manera divertida y conveniente.

Hay varias fuentes donde puedes encontrar recursos y ejercicios adicionales para practicar el uso del algoritmo de la división. Los libros de matemáticas, los sitios web educativos especializados y las aplicaciones móviles son excelentes opciones para ampliar tus conocimientos, obtener práctica adicional y fortalecer tus habilidades en esta importante técnica matemática. Así que no dudes en explorar estas fuentes y llevar tus habilidades en el algoritmo de la división al siguiente nivel.

Preguntas frecuentes (FAQ)

1. ¿Qué es el algoritmo de la división?

El algoritmo de la división es un procedimiento matemático que se utiliza para dividir dos números y obtener el cociente y el residuo.

2. ¿Cómo funciona el algoritmo de la división?

El algoritmo de la división consiste en repetir una serie de pasos: se divide el divisor entre la parte más significativa del dividendo, se multiplica el cociente obtenido por el divisor y se resta este resultado al dividendo original. Luego se baja un dígito del dividendo y se repite el proceso hasta que ya no se pueda seguir dividiendo.

3. ¿Cuándo se usa el algoritmo de la división?

El algoritmo de la división se utiliza en diversas situaciones como realizar operaciones aritméticas, simplificar fracciones, encontrar múltiplos o factores comunes, entre otros.

4. ¿Cuál es el residuo en el algoritmo de la división?

El residuo es el sobrante que queda después de realizar la operación de división. Es el resto de la división y siempre es menor que el divisor.

5. ¿Por qué es importante conocer el algoritmo de la división?

Es importante conocer el algoritmo de la división porque nos permite realizar cálculos precisos, entender mejor las propiedades numéricas y usarlo como herramienta para resolver problemas matemáticos.