Polígono no convexo: descubre todo sobre esta figura geométrica y sus propiedades

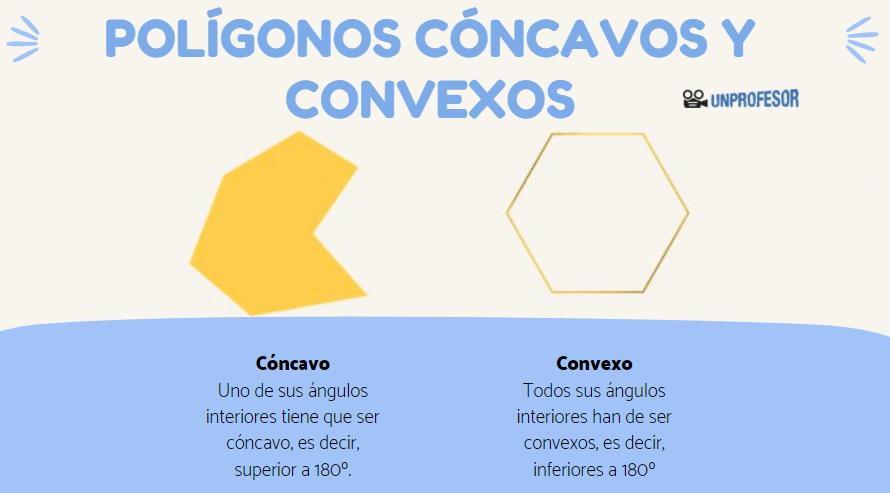
En el ámbito de la geometría, los polígonos son figuras planas que están compuestas por una serie de segmentos de recta consecutivos que forman un contorno cerrado. Existen distintos tipos de polígonos, siendo uno de ellos el polígono no convexo. A diferencia de los polígonos convexos, en los cuales todos sus ángulos internos miden menos de 180 grados, los polígonos no convexos presentan al menos un ángulo interno mayor a 180 grados.

Exploraremos las características y propiedades de los polígonos no convexos. Analizaremos cómo identificarlos, sus elementos y ángulos, así como también algunos ejemplos prácticos para comprender mejor su estructura. Además, veremos cómo se diferencian de los polígonos convexos y cuáles son algunas de las aplicaciones de estos polígonos en diferentes campos, como la arquitectura o la programación.

Qué es un polígono no convexo y cómo se diferencia de uno convexo

Un polígono no convexo es una figura geométrica que consta de al menos tres lados y cuyos ángulos internos en algún punto del polígono son mayores a 180 grados. A diferencia de un polígono convexo, que tiene todos sus ángulos internos menores o iguales a 180 grados, un polígono no convexo presenta una característica notable: contiene al menos un punto de su perímetro que está "hacia adentro" de la figura.

La principal diferencia entre un polígono no convexo y uno convexo radica en la forma en la que se curvan los lados de la figura. Mientras que en un polígono convexo los lados se curvan hacia afuera y se mantienen en el mismo lado del plano, en un polígono no convexo existe al menos un punto donde un lado cruza al otro, creando una especie de "intrusión" dentro de la figura.

Ejemplos de polígonos no convexos

Existen numerosos ejemplos de polígonos no convexos. Algunos de los más conocidos son:

1. El trapecio asimétrico: un trapecio en el que las bases no son paralelas, lo que provoca que al menos un vértice esté ubicado dentro de la figura.

2. El pentágono estrellado: un pentágono con lados largos que se cruzan en el centro, formando así cinco puntas en lugar de los tradicionales cinco ángulos rectos.

3. El hexágono cóncavo: un hexágono en el que uno de sus ángulos internos es mayor a 180 grados, lo que implica que al menos uno de sus lados formará una especie de "reentrante" en la figura.

Estos son solo ejemplos, pero los polígonos no convexos pueden tener cualquier cantidad de lados y formas diferentes. Cada uno de ellos presenta propiedades y características únicas que los hacen interesantes desde el punto de vista matemático y geométrico.

Propiedades de los polígonos no convexos

A diferencia de los polígonos convexos, los polígonos no convexos tienen ciertas propiedades particulares:

• No todos los lados del polígono están en el mismo lado del plano.

• Al menos un vértice del polígono se encuentra en el interior de la figura.

• Los ángulos internos en algún punto del polígono son mayores a 180 grados.

Estas propiedades hacen que los polígonos no convexos sean más complejos y difíciles de estudiar en comparación con los polígonos convexos. Sin embargo, también les otorgan una belleza e interés adicionales desde el punto de vista matemático.

Los polígonos no convexos son figuras geométricas que se diferencian de los polígonos convexos por la curvatura de sus lados y la presencia de al menos un punto interior en su perímetro. Estos polígonos presentan propiedades únicas, lo que los convierte en objetos fascinantes para el estudio matemático y geométrico.

Cuáles son las propiedades de un polígono no convexo

Un polígono no convexo es aquella figura geométrica en la cual al menos una de sus diagonales se encuentra fuera del polígono. A diferencia de un polígono convexo, que tiene todos sus ángulos internos menor a 180 grados, los polígonos no convexos presentan al menos un ángulo interno mayor o igual a 180 grados.

Una de las propiedades más destacadas de los polígonos no convexos es que no cumplen con el criterio de ser "estrellados". Esto quiere decir que no existe ninguna línea recta, llamada línea de estrellamiento, que una dos puntos en el interior del polígono sin intersectar ningún lado.

Descomposición en triángulos

Una de las características importantes de los polígonos no convexos es que pueden descomponerse en triángulos. Esta descomposición se logra trazando todas las diagonales dentro del polígono y formando triángulos con ellas.

La descomposición en triángulos permite analizar y estudiar las propiedades de los polígonos no convexos de manera más sencilla. Al descomponerlos en triángulos, se pueden aplicar distintos teoremas y fórmulas específicas para triángulos, lo que facilita el cálculo de áreas, perímetros, entre otras medidas.

Clasificación de los polígonos no convexos

Los polígonos no convexos se pueden clasificar en diferentes categorías según su forma y características. Algunos de los tipos más comunes son:

• Polígonos cóncavos: Son aquellos polígonos no convexos que presentan al menos un ángulo interno mayor a 180 grados.
• Polígonos estrellados: Son aquellos polígonos no convexos en los que existe al menos una línea recta que une dos puntos en el interior del polígono sin intersectar ningún lado.
• Polígonos cruzados: Son aquellos polígonos no convexos que se intersecan a sí mismos, es decir, presentan al menos un cruce entre sus lados.

Es importante tener en cuenta que los polígonos no convexos pueden presentar múltiples categorías al mismo tiempo, ya que pueden cumplir con más de una de las características mencionadas anteriormente.

Ejemplos de polígonos no convexos

Algunos ejemplos comunes de polígonos no convexos son:

1. Estrella de cinco puntas: Este polígono no convexo presenta cinco puntas o vértices y cinco lados. Cada vértice está conectado por una diagonal con los otros vértices que no son adyacentes.
2. Pentágono cruzado: Es un polígono no convexo que forma una especie de "". Los lados se cruzan entre sí, generando dos áreas diferentes en su interior.
3. Hexágono cóncavo: Un hexágono no convexo que presenta uno o más ángulos internos mayores a 180 grados.

Estos son solo algunos ejemplos de polígonos no convexos, pero existen muchas otras formas y combinaciones posibles que encajan dentro de esta clasificación.

Aplicaciones de los polígonos no convexos

Los polígonos no convexos tienen diversas aplicaciones en distintas áreas de estudio. Algunos ejemplos de estas aplicaciones son:

• Arquitectura: Los polígonos no convexos pueden utilizarse para diseñar estructuras y edificios con formas más complejas y llamativas.
• Robótica: En el campo de la robótica, los polígonos no convexos pueden ser utilizados como regiones de obstáculos o áreas de trabajo especiales para robots.
• Grafos: En matemáticas, los polígonos no convexos son utilizados como modelos para grafos direccionales y algoritmos relacionados con ellos.

Estos son solo algunos ejemplos, pero las aplicaciones de los polígonos no convexos son amplias y se extienden a diferentes campos de estudio e industrias.

Los polígonos no convexos son figuras geométricas con propiedades particulares, como su capacidad de descomposición en triángulos y su clasificación en distintas categorías según su forma. Estas figuras tienen diversas aplicaciones prácticas en áreas como la arquitectura, la robótica y las matemáticas, entre otras. Explorar y comprender las propiedades de los polígonos no convexos es fundamental para su estudio y aplicación en diferentes contextos.

Cuántos lados puede tener un polígono no convexo

Un polígono no convexo es una figura geométrica que tiene al menos un ángulo interno mayor a 180 grados. A diferencia de un polígono convexo, que tiene todos sus ángulos internos menores a 180 grados, el polígono no convexo puede tener una o más "concavidades". Estas concavidades se forman cuando al menos una de las líneas que conectan los puntos del polígono atraviesa su interior.

La cantidad de lados que puede tener un polígono no convexo es variada. No existe un límite máximo establecido, aunque es importante destacar que a medida que aumenta la cantidad de lados, la figura puede volverse más compleja y difícil de representar correctamente. Por lo tanto, si bien no hay un número máximo de lados definido, es común encontrarse con polígonos no convexos que tienen entre 4 y 10 lados.

En el caso de los polígonos no convexos con un número bajo de lados, como por ejemplo un cuadrilátero (4 lados) o un pentágono (5 lados), es más sencillo visualizar su concavidad. A medida que aumenta el número de lados, la figura se vuelve más intrincada y, en algunos casos, puede ser complicado identificar la presencia de concavidades a simple vista.

Ejemplos de polígonos no convexos

Para comprender mejor cómo lucen los polígonos no convexos, veamos algunos ejemplos:

• Estrella pentagonal: este polígono está formado por cinco segmentos de línea que se intersecan en el centro de la figura. Los ángulos internos de una estrella pentagonal son todos mayores a 180 grados, lo cual lo convierte en un polígono no convexo.
• Hexágono con un sesgo: un hexágono regular tiene todos sus ángulos internos iguales a 120 grados, pero si se modifica uno o más lados para crear una concavidad, se convierte en un polígono no convexo.
• Nonágono en forma de gancho: un nonágono regular, que tiene nueve lados y nueve ángulos internos iguales, puede convertirse en un polígono no convexo si se extiende uno de los lados del polígono hacia afuera, creando una gancho o una protuberancia.

Estos son solo algunos ejemplos, pero la cantidad de polígonos no convexos posibles es infinita. Como mencionamos anteriormente, cuanto mayor sea el número de lados, mayor será la complejidad de la figura y la dificultad para visualizar las concavidades.

Cuáles son los ejemplos más comunes de polígonos no convexos

Los polígonos no convexos son figuras geométricas que presentan al menos un ángulo interno mayor a 180 grados. A diferencia de los polígonos convexos, que tienen todos sus ángulos internos menores o iguales a 180 grados, los polígonos no convexos presentan una protuberancia en su forma.

Existen varios ejemplos comunes de polígonos no convexos, entre ellos se encuentran:

1. El trapecio con un ángulo obtuso

Un ejemplo de polígono no convexo es el trapecio con un ángulo interno mayor a 180 grados. Este tipo de trapecio puede tener dos pares de lados paralelos y uno de sus ángulos internos será mayor a 180 grados. Esta característica hace que el trapecio sea un polígono no convexo.

2. El romboide

Otro ejemplo de polígono no convexo es el romboide. El romboide es un paralelogramo con lados adyacentes desiguales y ángulos internos mayores a 180 grados. Sus diagonales se cruzan en puntos que no están dentro de la figura, lo cual indica que es un polígono no convexo.

3. El pentágono cóncavo

El pentágono cóncavo también es otro ejemplo de polígono no convexo. Un pentágono cóncavo es aquel que presenta al menos un ángulo interno mayor a 180 grados y uno o más lados que se curvan hacia el interior de la figura. Esto hace que su forma sea irregular y no convexa.

4. El estrella

El polígono estrella es otro ejemplo de polígono no convexo. Este tipo de polígono tiene una serie de triángulos en su interior y presenta ángulos internos mayores a 180 grados. Su forma se asemeja a una estrella y es considerado un polígono no convexo debido a su estructura.

Los polígonos no convexos son figuras geométricas que presentan al menos un ángulo interno mayor a 180 grados. Los ejemplos más comunes de polígonos no convexos incluyen el trapecio con un ángulo obtuso, el romboide, el pentágono cóncavo y el polígono estrella. Estos ejemplos muestran la diversidad que existe en la geometría y cómo las propiedades de los polígonos pueden variar tanto en su forma como en sus ángulos internos.

Cuáles son las principales características de un polígono no convexo

un polígono convexo.

Otro aspecto importante de los polígonos no convexos es que su perímetro no puede ser calculado mediante una fórmula sencilla como ocurre con los polígonos convexos. En su lugar, es necesario dividir el polígono no convexo en triángulos o trapecios más pequeños y calcular el perímetro de cada uno de ellos por separado.

Los polígonos no convexos pueden encontrarse en diferentes contextos, como la arquitectura, la geometría o incluso la naturaleza. Algunos ejemplos comunes de polígonos no convexos son las estrellas de mar, las letras cursivas, los mapas de países con islas o penínsulas, entre otros.

En resumen, un polígono no convexo se diferencia de un polígono convexo por tener al menos un ángulo interno mayor a 180 grados y presentar áreas cóncavas en su interior. Su forma irregular y la presencia de diagonales exteriores son características distintivas de este tipo de polígonos. Además, su perímetro debe calcularse dividiendo la figura en triángulos o trapecios más pequeños. Los polígonos no convexos se encuentran en diversos ámbitos y pueden presentarse en diferentes formas y tamaños.

Cuáles son las fórmulas para calcular el área y el perímetro de un polígono no convexo

o y sumarlas para obtener el perímetro total. Es importante destacar que debido a la presencia de ángulos internos mayores a 180 grados, los polígonos no convexos presentan una mayor complejidad en el cálculo de su área y perímetro.

Cuáles son algunas aplicaciones prácticas de los polígonos no convexos en la vida diaria

Los polígonos no convexos son figuras geométricas que presentan al menos un ángulo interior mayor a 180 grados. Mientras que los polígonos convexos tienen todos sus ángulos interiores menores a 180 grados, los polígonos no convexos pueden tener alguno o varios ángulos mayores a esta medida.

En la vida diaria podemos encontrar diversas aplicaciones prácticas de los polígonos no convexos. A continuación, te presentaremos algunas de ellas:

Diseño arquitectónico

En el mundo de la arquitectura, los polígonos no convexos pueden ser utilizados para crear estructuras y edificaciones con formas innovadoras y llamativas. Estos polígonos permiten diseñar espacios únicos que rompen con la tradicionalidad de las formas rectas y regulares de los polígonos convexos. Las fachadas de algunos edificios famosos, como el Museo Guggenheim en Bilbao o la Ópera de Sídney, son ejemplos de este tipo de diseños arquitectónicos que hacen uso de los polígonos no convexos.

Juegos y puzzles

Los polígonos no convexos también tienen su lugar en el entretenimiento. En los juegos y puzzles geométricos, estos polígonos desafían nuestra lógica y habilidades visuales. Rompecabezas como el tangram, que consiste en un conjunto de polígonos no convexos, ofrecen horas de diversión mientras intentamos encontrar diferentes formas utilizando todas las piezas dadas.

Modelado 3D

En el ámbito del modelado 3D, los polígonos no convexos son ampliamente utilizados para representar objetos con formas más complejas. Estos polígonos permiten crear modelos más detallados y realistas de personajes, escenarios y objetos virtuales. Los videojuegos y las películas animadas son ejemplos de industrias en las que se hace uso intensivo del modelado 3D con polígonos no convexos.

Geografía y cartografía

En la geografía y la cartografía, los polígonos no convexos son utilizados para representar formas irregulares de terrenos, cuerpos de agua y regiones geográficas. Estos polígonos permiten hacer mapas más precisos y detallados, mostrando con mayor exactitud los contornos de islas, bahías, ríos y montañas, por ejemplo.

Los polígonos no convexos tienen diversas aplicaciones prácticas en nuestra vida diaria. Desde el diseño arquitectónico hasta la representación de objetos en el mundo virtual, estos polígonos ofrecen posibilidades creativas y funcionales para diferentes disciplinas. Explorar y comprender las propiedades de los polígonos no convexos nos permite apreciar la belleza de la geometría y cómo influye en nuestro entorno cotidiano.

Cuáles son algunas estrategias para identificar y clasificar un polígono como convexo o no convexo

Para identificar y clasificar un polígono como convexo o no convexo, existen diversas estrategias que pueden ayudarnos a determinar correctamente la naturaleza de la figura geométrica en cuestión. A continuación, te mencionaré algunas de las estrategias más comunes utilizadas por los matemáticos y expertos en geometría.

Análisis de ángulos internos

Una forma de identificar si un polígono es convexo o no es mediante el análisis de sus ángulos internos. En un polígono convexo, todos sus ángulos internos deben ser menores a 180 grados. En cambio, en un polígono no convexo, encontraremos al menos un ángulo interno que es mayor o igual a 180 grados.

Dibujo de diagonales

Otra estrategia es dibujar las diagonales del polígono y analizar su posición con respecto al polígono. En un polígono convexo, todas las diagonales se encontrarán completamente dentro del polígono. Mientras tanto, en un polígono no convexo, al menos una diagonal cruzará fuera de la figura, extendiéndose más allá de los límites del polígono.

Prueba de puntos extremos

La prueba de puntos extremos también es útil para clasificar un polígono como convexo o no convexo. Consiste en seleccionar dos puntos extremos en el polígono y trazar una línea recta que los conecte. Si esta línea recta se encuentra completamente dentro del polígono, entonces el polígono es convexo. En cambio, si la línea recta se sale del polígono en algún punto, entonces el polígono es no convexo.

Examen de lados consecutivos

Otra estrategia consiste en examinar los lados consecutivos del polígono. En un polígono convexo, todos los segmentos de línea que conectan dos vértices consecutivos del polígono deben estar completamente dentro del polígono. Si al menos un segmento de línea cruza fuera de los límites del polígono, entonces el polígono es no convexo.

Estas estrategias son algunas de las maneras más comunes de identificar y clasificar polígonos como convexos o no convexos. Sin embargo, es importante recordar que cada caso puede ser único y requerir diferentes enfoques para llegar a una conclusión precisa sobre la naturaleza del polígono.

Cuáles son los problemas matemáticos asociados con los polígonos no convexos

Los polígonos no convexos, también conocidos como polígonos cóncavos, son figuras geométricas que presentan al menos un ángulo interno mayor a 180 grados. A diferencia de los polígonos convexos, en los cuales todos los ángulos internos son menores a 180 grados, los polígonos no convexos poseen una forma más irregular y pueden presentar lados que se cruzan entre sí.

Estas características particulares hacen que los polígonos no convexos sean objeto de estudio e investigación en la rama de la matemática conocida como geometría. Diversos problemas matemáticos están asociados con estas figuras geométricas, y su comprensión es fundamental para resolverlos correctamente.

Uno de los principales problemas matemáticos relacionados con los polígonos no convexos es el cálculo del área.

Calcular el área de un polígono no convexo puede resultar un desafío debido a su forma irregular y a la presencia de ángulos internos mayores a 180 grados. En estos casos, se requiere abordar el problema dividiendo el polígono en triángulos o en partes más simples que permitan calcular las áreas de forma individual y posteriormente sumarlas.

La utilización de fórmulas específicas para cada tipo de polígono no convexo puede ser de gran ayuda en el cálculo del área. Sin embargo, la complejidad de algunos polígonos no convexos puede hacer necesario recurrir a métodos numéricos o aproximaciones para obtener una estimación del área con cierta precisión.

Otro problema matemático relacionado con los polígonos no convexos es la determinación de la existencia de diagonales.

Las diagonales son segmentos que unen dos vértices no consecutivos de un polígono. En el caso de los polígonos no convexos, no todos los vértices pueden ser conectados por diagonales. La presencia de lados que se cruzan entre sí dificulta la trazabilidad de dichas diagonales y plantea interrogantes sobre su existencia.

Determinar si un polígono no convexo admite o no diagonales implica analizar las condiciones geométricas que cumplen los lados del polígono. Teoremas específicos, como el Teorema de Jordan, pueden ser utilizados para establecer criterios que determinen la existencia de diagonales en estos polígonos y ayuden a resolver este problema matemático.

Además del cálculo del área y la determinación de diagonales, otro problema matemático relevante asociado a los polígonos no convexos es la clasificación de sus ángulos internos.

La clasificación de los ángulos internos de un polígono no convexo es esencial para comprender su estructura y geometría. Dependiendo de la medida de los ángulos internos, los polígonos no convexos pueden dividirse en subcategorías como los polígonos bicóncavos (todos los ángulos internos son mayores a 180 grados) estrictamente cóncavos (al menos un ángulo interno mayor a 180 grados pero no todos) y múltiplemente cóncavos (con múltiples ángulos internos mayores a 180 grados).

Resolver el problema de la clasificación de los ángulos internos en polígonos no convexos implica analizar las medidas de los ángulos y establecer criterios que permitan categorizarlos correctamente. Mediante el uso de conceptos como ángulos suplementarios, complementarios y conocimientos de trigonometría, es posible determinar si un ángulo interno dado pertenece a una subcategoría específica de polígono no convexo.

Los polígonos no convexos presentan diversos problemas matemáticos que requieren de un análisis detallado y técnicas específicas para su resolución. El cálculo del área, la determinación de diagonales y la clasificación de los ángulos internos son solo algunos ejemplos de los desafíos que plantea el estudio de estas figuras geométricas. A través de la utilización de herramientas y teoremas matemáticos, es posible comprender y resolver estos problemas, ampliando nuestro conocimiento en el campo de la geometría y la matemática.

Cuáles son los conceptos relacionados, como el ángulo de reflexión y las diagonales internas, que se aplican a los polígonos no convexos

Los polígonos no convexos son figuras geométricas que presentan al menos una diagonal interna que se encuentra fuera de la figura. A diferencia de los polígonos convexos, estos polígonos no tienen todos sus ángulos internos menores a 180 grados y pueden tener lados que se curven hacia adentro.

Una de las propiedades más destacadas de los polígonos no convexos es su angulo de reflexión. El ángulo de reflexión es aquel formado por la prolongación de un lado del polígono con la diagonal interna que no está dentro de la figura. Este ángulo puede variar dependiendo de la forma y estructura del polígono, lo que hace que cada polígono no convexo sea único.

Otra propiedad interesante de los polígonos no convexos son sus diagonales internas. A diferencia de los polígonos convexos, estos polígonos pueden tener diagonales internas que no cruzan el interior de la figura, sino que atraviesan espacios vacíos entre los lados del polígono. Estas diagonales pueden ser de diferentes longitudes y direcciones, lo que contribuye a la complejidad y diversidad de los polígonos no convexos.

Relación entre los polígonos no convexos y otros conceptos geométricos

Los polígonos no convexos están estrechamente relacionados con otros conceptos geométricos, como los polígonos convexos y los polígonos regulares.

En comparación con los polígonos convexos, los polígonos no convexos presentan una mayor variabilidad de formas y pueden tener un número diferente de lados. Mientras que los polígonos convexos tienen todos sus ángulos internos menores a 180 grados y sus diagonales internas completamente dentro de la figura, los polígonos no convexos desafían estas reglas y pueden presentar características únicas en términos de ángulos y diagonales.

Por otro lado, los polígonos regulares también se diferencian de los polígonos no convexos. Los polígonos regulares son aquellos que tienen todos sus lados y ángulos iguales. En contraste, los polígonos no convexos pueden tener lados de diferentes longitudes y ángulos internos variados. Esto genera una mayor diversidad de formas y estructuras en los polígonos no convexos en comparación con los polígonos regulares.

Ejemplos de polígonos no convexos en la vida cotidiana

Aunque los polígonos no convexos pueden parecer figuras abstractas, en realidad se encuentran en muchos objetos y situaciones de la vida cotidiana.

• En arquitectura, algunos edificios pueden tener diseños que incluyen polígonos no convexos. Por ejemplo, el Museo Solomon R. Guggenheim en Nueva York presenta una forma de polígono no convexo, con una base circular y una estructura que se ensancha hacia arriba.
• En diseño de productos, es común encontrar formas no convexas en herramientas o utensilios, como destornilladores o abrelatas, que están diseñados para cumplir una función específica y requieren una forma no estándar para cumplir su propósito.
• En el arte y la ilustración, los polígonos no convexos pueden ser utilizados como elementos visuales interesantes. Por ejemplo, en el diseño gráfico se pueden utilizar polígonos no convexos para crear composiciones abstractas o para destacar ciertas áreas de una imagen.

Los polígonos no convexos son figuras geométricas que presentan características únicas en términos de ángulos y diagonales internas. Estas figuras desafían las reglas de los polígonos convexos y pueden encontrarse tanto en objetos cotidianos como en obras arquitectónicas o en el arte visual. Su análisis y estudio contribuyen al entendimiento de la geometría y su aplicación práctica en diversas disciplinas.

Cuáles son las formas de utilizar los polígonos no convexos en el diseño gráfico y la arquitectura

Los polígonos no convexos son figuras geométricas que presentan al menos un ángulo interno mayor a 180 grados. A diferencia de los polígonos convexos, los polígonos no convexos tienen lados que se "hunden" hacia el interior de la figura en lugar de "salir" hacia el exterior.

Estas figuras geométricas pueden ser muy interesantes y versátiles a la hora de utilizarlos en el diseño gráfico y la arquitectura. Su forma única y distintiva puede agregar un toque de originalidad y creatividad a cualquier proyecto.

En el diseño gráfico, los polígonos no convexos se utilizan para crear composiciones visuales impactantes y llamativas. Su estructura peculiar permite jugar con diferentes perspectivas y áreas negativas, lo que resulta en diseños visualmente atractivos y dinámicos. Estas figuras geométricas son especialmente populares en el diseño de logotipos, carteles y piezas publicitarias.

Además, los polígonos no convexos también pueden darle profundidad e intensidad a ilustraciones y gráficos digitales. Al combinar diferentes formas y colores, es posible crear efectos tridimensionales que capturan la atención del espectador y generan una sensación de movimiento. Esto es especialmente útil en la creación de animaciones y videos promocionales.

En el campo de la arquitectura, los polígonos no convexos ofrecen un medio de expresión artística y creativa para los diseñadores. Al incorporar estas formas geométricas en la estructura y fachada de un edificio, se puede lograr una apariencia única y vanguardista. Los polígonos no convexos permiten jugar con las líneas y los planos, creando efectos visuales sorprendentes y añadiendo un componente escultural al diseño arquitectónico.

Además de su valor estético, los polígonos no convexos también pueden tener aplicaciones prácticas en la arquitectura. Por ejemplo, estos polígonos se utilizan para diseñar espacios interiores que requieren una división inteligente y eficiente del espacio. Al utilizar paredes curvas o inclinadas, se puede crear ambientes dinámicos y fluidos que mejoran la funcionalidad y la experiencia del usuario.

Los polígonos no convexos son figuras geométricas que ofrecen un sinfín de posibilidades en el diseño gráfico y la arquitectura. Su forma peculiar y distintiva permite crear composiciones visuales impactantes y diseños arquitectónicos vanguardistas. Ya sea utilizado en logotipos, carteles, edificios o espacios interiores, los polígonos no convexos añaden un toque de originalidad y creatividad a cualquier proyecto.

Cómo se pueden describir los polígonos no convexos en términos de sus propiedades angulares y laterales

Los polígonos no convexos son figuras geométricas que presentan al menos una línea conectando dos puntos interiores que se encuentra fuera de la figura. A diferencia de los polígonos convexos, que no tienen ninguna línea que atraviese su interior, los polígonos no convexos pueden tener una o más líneas secantes.

Para describir los polígonos no convexos en términos de sus propiedades angulares y laterales, debemos analizar tanto los ángulos como las longitudes de sus lados. En este tipo de polígonos, puede haber ángulos internos mayores a 180 grados y lados intersectados que se cruzan en su interior.

Propiedades angulares

En un polígono no convexo, los ángulos internos pueden ser clasificados en tres categorías: agudos, obtusos y reflex. Los ángulos agudos miden menos de 90 grados, los ángulos obtusos miden más de 90 grados pero menos de 180 grados, mientras que los ángulos reflex son aquellos que miden más de 180 grados.

Además, es importante mencionar que en un polígono no convexo la suma de todos los ángulos internos no es igual a (n-2) * 180 grados, como ocurre en los polígonos convexos. Esta característica es una de las principales diferencias entre ambos tipos de polígonos.

Propiedades laterales

En cuanto a los lados de los polígonos no convexos, estos pueden cruzarse o intersectarse en su interior. Esta condición se da cuando dos lados comparten un punto en común y se cruzan entre sí. A diferencia de los polígonos convexas, donde los lados no se intersectan y solo comparten puntos en los vértices.

Otra propiedad interesante es la presencia de "cúspides" o "puntas" en un polígono no convexo. Las cúspides son vértices que sobresalen hacia el exterior del polígono, lo cual da una forma más irregular y menos uniforme a la figura.

Ejemplos de polígonos no convexos

A continuación, presentaremos algunos ejemplos de polígonos no convexos:

• Estrella pentagonal.
• Estrella hexagonal.
• Estrella octogonal.
• Herradura.

Estos ejemplos ilustran cómo los polígonos no convexos pueden presentar diferentes configuraciones de ángulos y lados, lo que les confiere su naturaleza no convexa.

Los polígonos no convexos son figuras geométricas que se caracterizan por tener al menos una línea que atraviesa su interior. Sus propiedades angulares y laterales nos permiten diferenciarlos de los polígonos convexos y entender sus características únicas. Además, su forma irregular y la presencia de cúspides los distingue visualmente de otras figuras geométricas convexas.

Preguntas frecuentes (FAQ)

1. ¿Qué es un polígono no convexo?

Un polígono no convexo es una figura geométrica que tiene al menos un ángulo interno mayor de 180 grados.

2. ¿Cuál es la diferencia entre un polígono convexo y uno no convexo?

La principal diferencia radica en los ángulos internos. En un polígono convexo, todos los ángulos internos son menores o iguales a 180 grados, mientras que en un polígono no convexo existe al menos un ángulo interno mayor a 180 grados.

3. ¿Cuántos lados puede tener un polígono no convexo?

Un polígono no convexo puede tener cualquier cantidad de lados, siempre y cuando cumpla con la condición de tener al menos un ángulo interno mayor a 180 grados.

4. ¿Cuáles son las propiedades de un polígono no convexo?

Algunas de las propiedades de los polígonos no convexos son: tienen al menos un ángulo interno mayor a 180 grados, sus diagonales pueden intersectarse en su interior y no todas las diagonales estarán dentro del polígono.

5. ¿Cuál es un ejemplo famoso de polígono no convexo?

Uno de los ejemplos más conocidos de polígono no convexo es el pentágono irregular, en el cual dos de sus ángulos internos miden 216 grados y los otros tres miden 108 grados.